3. MEASUREMENT
Measurement is the process of assigning numbers and units to a given event or observation.
Example:
-
Length of a book is 25cm
-
An angle of 300
Consider the fact that if we say the length of a pen is 25 cm “ 25 gives the answer for how much” and “cm” gives the answer for “of what”.
PHYSICAL QUANTITIES
In physics whatever we measure is referred as a physical quantity.
Physical quantity is something that we can measure in Physics.
This includes:Mass, time, length, volume, area, pressure, temperature etc
Each of these physical quantities may be measured by using one or more units. Internationally each physical quantity is assigned with its single unit which is recognized. These are the standard international unit (SI units) or system of international unit.
There are two types of physical quantities;
1. Fundamental physical quantity
2. Derived physical quantity
Fundamental physical quantities are those which can not be expressed in terms of other physical quantities namely;
1. Mass
2. Length
3. Time
4. Thermodynamic Temperature
5. Electric current
6. Luminous intensity
7. Amount of substance
Three Basic Fundamental Quantities
There are three basic fundamental quantities which are mass, length and time.
THE SI
The SI is the system of units used by Scientists worldwide. SI stands for Systemè de International.
Basic Physical quantities and their SI units
|
Basic physical quantities |
SI unit |
Symbol |
|
Mass |
Kilogram |
Kg |
|
Length |
Meter |
m |
|
Time |
Second |
s |
Standard multiplication Fracture;
|
Multiplication future |
POWER |
Prefix |
Symbol |
|
1000000000000 |
1012 |
Tera |
T |
|
1000000000 |
109 |
Giga |
G |
|
1000000 |
106 |
Mega |
M |
|
1000 |
103 |
Kilo |
K |
|
100 |
102 |
Hecto |
H |
|
10 |
10 |
Deca |
Da |
|
1 |
- |
- |
- |
|
|
1 |
- |
- |
|
0.1 |
10-1 |
Deci |
D |
|
0.01 |
10-2 |
Cent |
C |
|
0.001 |
10-3 |
Millis |
Ml |
|
0.000001 |
10-6 |
Micro |
µ |
|
0.000000001 |
10-9 |
Nano |
|
|
0.000000000001 |
10-12 |
Pico |
NB: International systems of unit (SI unit) - are units which are uniform all over the world.
MEASUREMENT OF LENGTH
-
Length - is the distance between two points. It is one of the three fundamental (basic) physical quantities used in mechanics.
The SI unit of length is the meter (m) Other units of length are;
- 1 kilometer (km)=1000 meter
- 1 hectometer (hm)= 100 meter
- 1 decameter (dam) = 10 meter
- 1 decimeter (dm) = 10-1 or 0.1 meter
- 1 centimeter (cm) = 10-2 or 0.01 meter
- 1 millimeters (mm) = 10-3 or 0.001 meter
INSTRUMENTS USED TO MEASURE LENGTH.
There are number of instruments used for accurate measurement of length.The choice of instrument is determined by of the object to be measured.
Examples of those instruments are;
-
Meter rule
-
Tape measure
-
Vernier caliper
-
Micrometer screw gauge
USING A METER RULE TO MEASURE LENGTH
-
A meter rule measures length of the order of 100cm.
-
When measuring length of unknown object, the correct way of reading is by looking straight and perpendicular to the point. Side way observation leads to very answer.
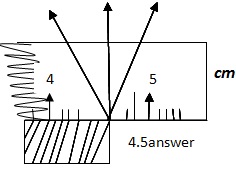
Errors
In measurement the devotion from the true reading is called error.
VERNIER CALIPER
A vernier caliper is used to measure short distance of the order of 10cm (the accuracy of 0.01cm).
For example; diameter of pen, ball or pendulum bob.
It consists of two scales:
-
The main scale
-
The vernier scale
• It also has the inside jaws and outside jaws.
The inside jaw is used to measure the internal diameter of a tube and outside jaw is for external diameter.
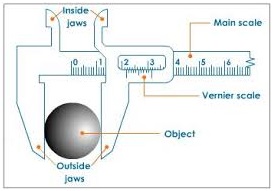
How to take readings of the vernier calipers. There are two parts which are used in taking readings;
-
Main scale
-
Vernier scale
1 main scale mark = 0.1 cm or 0.01 mm
1 Vernier scale mark = 0.01 cm or 0.001 mm
The reading is usually taken where the main scale mark coincides with the Vernier scale mark.
NB: When the main scale mark and Vernier scale mark do not coincide the reading may be taken with the first, second, third or fourth vernier mark.
Examples;
1.Determine the reading of the following Vernier calipers.
Readings
Main scale = 6.00 cm
Vernier scale = + 0.08 cm
Reading = 6.08 cm.
2. Determine the reading of the Vernier caliper shown.
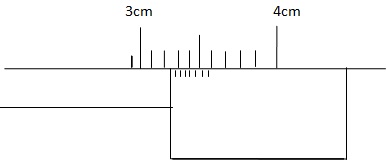
Readings:
Mean scale 3.20 cm
Vernier scale + 0.04 cm
Reading 3.24 cm
3. Determine the reading of vernier caliper shown.
Solution:
Since No mean scale mark and vernier scale mark concedes then the reading is under;
Mean scale = 8.70 or 8.70 or 8.70 or 8.70
Vernier scale= +0.01 +0.02 + 0.03 +0.04
Reading = 8.71 8.72 8.73 8.74
4. Determine the reading of vernier caliper
object
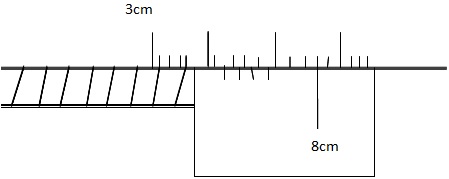
Reading Main scale = 3.40cm
Vernier scale = +0.08 cm
Reading = 3.48 cm
THE MICROMETER SCREW GAUGE
The micrometer screw gauge is an instrument used to measure a length to an accuracy of 0.001cm (or 0.01 mm).
It is used for measuring the diameter of wires and ball bearing. It is capable to measure small length up to about 2.5 cm.
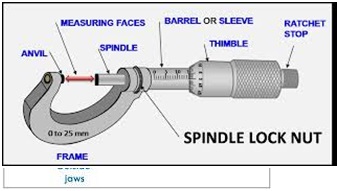
It consists of;
-U-shaped frame (F)
-Anvil (A)
-Spindle (P)
-Sleeve (E)
-Thimble (T)
-Ratchet (R)
How to take readings using micrometer screw gauge
Two principle parts are used for taking reading;
-
Sleeve (E)
-
Thimble ( T)
NOTE: 1 sleeve mark = 0.01 cm or 0.1 mm
1 Thimble mark = 0.001 cm or 0.01 mm.
-
In sleeve if the lower sleeve mark is between the thimble margin and upper sleeve mark, the lower sleeve mark is read as 0.5mm or 0.05 cm and added to the upper sleeve reading to get sleeve reading.
1. Sleeve reading
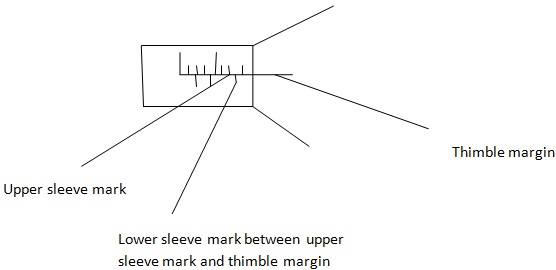
The sleeve reading;
4+0.5mm
- In contrast if the lower sleeve mark is not between the thimble margin and the upper sleeve we don’t count the lower sleeve mark to the sleeve reading.
Example:
1. What is the reading of the following micrometer screw gauge below?
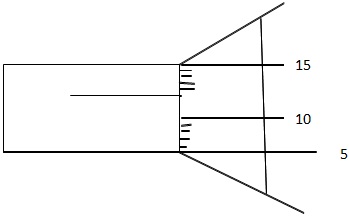
Solution:
Sleeve reading = 5.50 mm
Thimble reading = +0.12 mm
Total reading = 5.62 mm.
2. Give the reading of micrometer screw gauge below;

Solution:
Sleeve reading = 3.00 mm
Thimble reading = + 0.48mm
Total reading = 3.48 mm
EXERCISE
1. Determine the reading of micrometer screw gauge below;
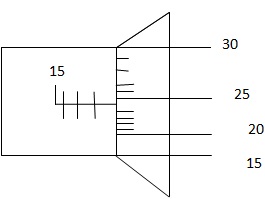
Solution:
Sleeve reading 17.50mm
Thimble reading + 0.24 mm
Total reading = 17.74mm
MEASUREMENT OF MASS
Mass - is a quantity of matter / body it contains e.g. when we buy some flour at the shop, we buy a quantity or certain amount of flour. This is a mass of flour.
The SI unit of mass is kilogram (kg).
Other units of mass include the following;
- 1 Kilogram (kg) = 1000g
- 1 Hectogram (Hg) = 100g
- 1 decagram (dag) = 10g
- 1 Decigram (dg) = 0.1g
INSTRUMENTS USED TO MEASURE MASS
Mass is measured by a beam balance. Other instruments used to measure mass are Triple beam balance, chemical balance and digital balance.
The following are the types of beam balance;
-
Triple – beam balance
-
Chemical beam balance
-
Digital balance
-
Roman steel yard beam balance
Example of beam balance:

MASS AND WEIGHT
Many people got confused of these two terms they think that mass and weight is the same but in reality they have two(2) different meaning.
| MASS | WEIGHT |
|
-It is a force of attraction on bodies towards the earth center. |
|
-Its SI unit is Newton (N) |
|
-It is measured by spring balance. |
|
-It changes from one place to another |
|
-It is vector quantity |
|
-It is a derived physical quantity |
MEASUREMENT OF TIME
Time - Is the interval between two events used to record the duration of events taking places between them.
•The SI unit of time is second (s).
•Other units of time include;
•Minutes: 1 minute = 60 seconds
•Hours: 1 hour =60 minutes also1 hour = 3600 seconds
•Days: 1 day = 24 hours
•Weeks: 1 week = 7 days
•Months: 1 month = 4 weeks
•Years: 1 year = 12 months
•Decades: 1 decade = 10 years
•Century: 1 century = 100 years
•Millennium - 1 millennium = 1000 years
INSTRUMENT USED TO MEASURE TIME
Time is precisely measured by using stop watch.
Stop watches are of two kinds:
-
Mechanical stop watch
-
Digital stop watch.


DERIVED PHYSICAL QUANTITIES
These are physical quantities which can be expressed in terms of other physical quantities
They include;
-
Volume
-
Density
-
Relative density
-
Force
-
Velocity
-
Acceleration
-
Speed
-
Work
-
Energy
-
Power etc.
MEASUREMENT OF VOLUME
Volume - is the amount of space occupied by a substance.
The SI unit of volume is meter cubic (m3) other unit of volume includes liters (l), cubic centimeter (cm3), milliliter (m) etc.
DETERMINATION OF VOLUME OF SUBSTANCES
•A VOLUME OF SOLID
Solid have been divided into two categories;
-
Regular solid
This is the solid which has both definite shape and size e.g. spheres, cylinder, squares, etc.
-
Irregular solid
This solid which has neither definite shape nor size e.g. stones.
•VOLUME OF REGULAR SOLIDS
For example these can be found by a formula;
-
Cylinder
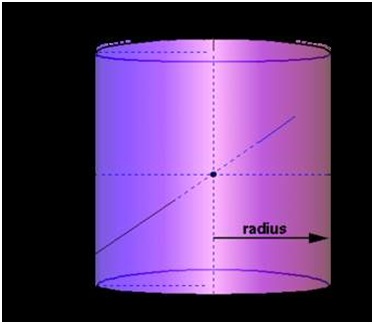
V= πr2l
where
r=radius
=or 3.14
L=length
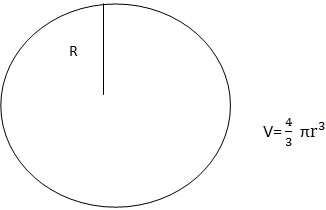
2. Sphere
3. Rectangular block
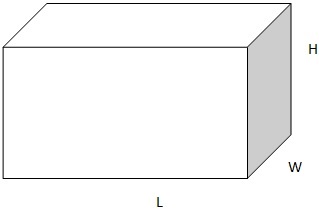
V= l x h x w
Where l= length
w= width
h= height
Example
1. A cylinder pipe has a radius of 7cm and is 20cm long. Calculate its volume.
Data:
R=7cm
L= 20 cm
V=?
Solution
V =πlr2
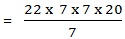
V =3080 cm3
Example 2
A spherical bob has a radius of 0. 7cm. Calculate its volume.
Data
R= 0.7cm
V=?
Solution
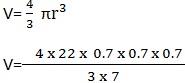
Volume = 1.4373 cm3
Example 3
Rectangular block has a length of 2cm, width of 4cm and height of 12 cm. Calculate its volume.
Data
Length = 2cm
Width = 4cm
Height = 12cm
Volume =?
Solution
V = l × w × h
= 2×4×12 =96 cm3
Volume = 96 cm3
VOLUME OF IRREGULAR SOLID
The volume of these solids is obtained by using displacement method as shown.
-
Fill measuring cylinder with water and record it is volume say v1
-
Lower a store with threads into the cylinder and record the new volume say v2.
-
The volume of stone v = v2 - v1
Diagram

Example:
A measuring cylinder is filled with water to a volume of 20cm3. When the stone immersed the volume raised to 38cm3. Calculate volume of a stone.
Data:
V1 = 20 cm3
V2 = 38 cm3
since: V2-V1
∴38 -20 = 18cm3
DENSITY AND RELATIVE DENSITY
Density: Is the mass of substance per unit of volume.

ρ = Symbol for density (Greek letter, rho)
M= mass
V= volume
The SI unit of density is kilogram per cubic meter (kg/m3)
It’s true to say;
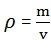
And hence

Other unit of density is gram per cubic centimeter (g/ cm3)
Example
1. Find the density of a body with mass of 200kg and volume of 10m3
Data:
Mass (m) = 200kg
Volume (v) = 10m3
Density =?
Solution
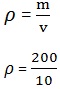
= 20kg m3
Example
2. A body has a mass of 40kg and a volume of 5m3 calculate its density.
Data:
Mass (m) = 40kg
Volume (v) = 5m3
Density =?
Solution
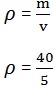
= 8kg/m3
Density = 8kg/m3
Example
3. A body has a mass of 40kg and volume of 0.4m3. Calculate its density.
Data:
Mass (m) = 40 kg
Volume (v) =0.4m3
Formula:
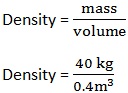
Density=100kg/m3
Exercise
-
A block of wood of volume 60cm3 has a mass of 45g. Find the density of wood.
Data:
Mass (m) = 45g
Volume (v) = 60cm3
Density =?
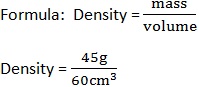
Density=0.75g/cm3
2. The density of mercury is 13.6g/cm3. Find the volume if the mass of mercury is 204 gram.
Data:
Mass (m) = 204g
Volume (v) = ?
Density = 13.6g/cm3
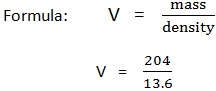
V= 15cm3
3. A body has a density of 0.9g/cm3 if the volume of that body is 6cm3. Find its mass.
Data:
Mass (m) =?
Volume (v) = 6cm3
Density = 0.9g/cm3
Solution: m= 0.9g/cm3 × 6cm3
= 0.54g/cm3
mass =0. 54cm3
DETERMINATION OF DENSITY OF LIQUID
Procedure
Find the mass of an empty dry beaker then pour it into a known volume of liquid by using a pipette.Find the mass of beaker of liquid.
Result:
Mass of empty beaker = (m1)
Mass of beaker and liquid = m2
Volume of liquid = v
Mass of liquid = m2—m1
Density of liquid = ( m2—m1 ) g /cm3 or kg /m3
Example:
1. A Clean beaker has a mass of 100g. A volume of 100cm3 of liquid is poured into the beaker with the help of a pipette. The mass of beaker and its contents is 140g. Calculate the density of liquid.
Data:
Mass of empty beaker (m1) = 100g
Mass of beaker and liquid (m2) = 140g
Volume of liquid = 100cm3
Density of liquid = ?
Solution:
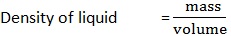
But mass = m2 - m1
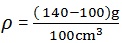
Density of liquid = 0.4g/cm3
Example 2:
A clean beaker has a mass of 500g. A volume of 25cm3 of liquid is poured into the beaker with the help of pipette. The mass of beaker and its contents is 600g. Calculate the density of liquid.
Mass of empty beaker (m1) = 500g
Mass beaker and liquid (m2) = 600g
Volume liquid = 25cm3
Density of liquid = ?
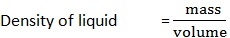
But mass = m2 — m1
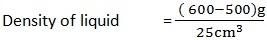
Density of liquid = 4 g/cm3
RELATIVE DENSINTY (RD)
Definition:
Relative density is the ratio of a density of a substance to the density of liquid.
OR
Relative density is the ratio of mass of substance to the mass of equal volume of liquid.
-
Since the density of water is 1g/cm3 or 1000kg /m3 .It is common to compare density of substance to that of water.
-
This comparison is what we call relative density (RD). Relative density has no unit because it is the ratio of two equal quantities.
mathematically;
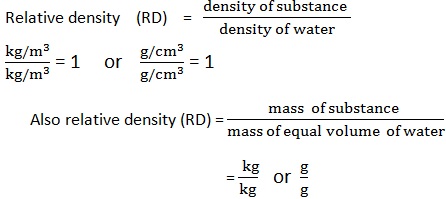
Example
1. The iron metal has a density of 2700kg/m3. Find its relative density if the density of water is 1000kg/m3.
Data:
Density of iron = 2700kg/m3
Density of water = 1000kg/m3
Relative density (Rd) =?
Solution
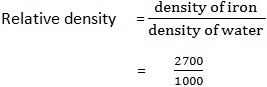
= 2.7
2. If the mass of copper is 3600kg and mass of water is 2500kg. Find the relative density of copper.
Solution:
Mass of copper = 3600kg
Mass of water = 2500kg
Relative density = ?
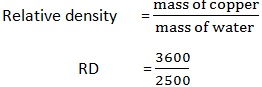
RD= 1.44
3. An object has a mass of 50g and a volume of 20cm3. Find the relative density of object
Data:
Density of mass = 50g
Density of volume = 20cm3
Relative density (RD) =?
Solution:
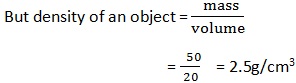
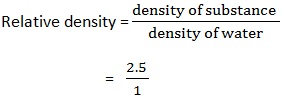
=2.5
RELATIVES DENSITY OF LIQUID
The relative density of liquid can be easily determined by using a relative density bottle.
Procedure:
-
Find the mass of an empty dry of density bottle - m1
-
Fill the bottle with liquid then record its mass -m2
-
Empty the bottle and raise its water.
-
Fill the bottle with water and find its mass after drying with a blotting paper m3.
Results:
-
Mass of liquid = m2 — m1
-
Mass of water = m3 — m1
Example.
1. A relative density bottle has a mass of 29.2g when dry and empty. Its mass is 116.2 g when full of liquid (diesel) and when full of water its mass is 129.2g. Calculate the relative e density of diesel.
Data:
Mass of empty bottle (m1) = 29.2 g
Mass of diesel (m2) = 116.2 g
Mass of water (m3) = 129.2g
Solution:
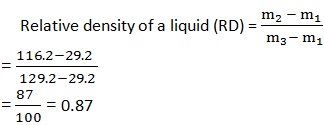
The relative density of diesel is 0.87
APPLICATIONS OF DENSITY IN DAILY LIFE
1.Design of sheep and planes
2. Relative density is used to determine density of unknown substance
3. To identify gemstones
4. Density is considered in designing of swimming equipments